AOJ 2167 : Find the Point
問題リンク : Find the Point | Aizu Online Judge
問題概要 :
n本の直線が与えられる
それら全ての直線への最短距離が等しい点を見つけよ
そのような点が複数ある場合は "Many" と出力し、
1つも存在しない場合は "None" と出力せよ
解法 :
まず、直線が2本だけの場合を考える
2本の直線が平行な場合、それらの直線から等しい距離にある点は以下の図の点線の部分になる
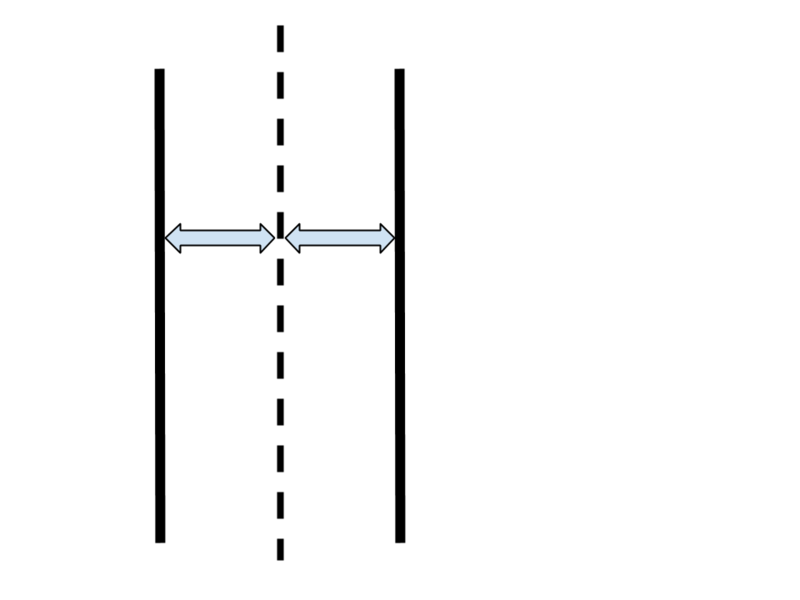
2本の直線が平行でない場合、それらの直線から等しい距離にある点は以下の図の点線の部分になる
同じ色の矢印が示す部分の角度は等しい
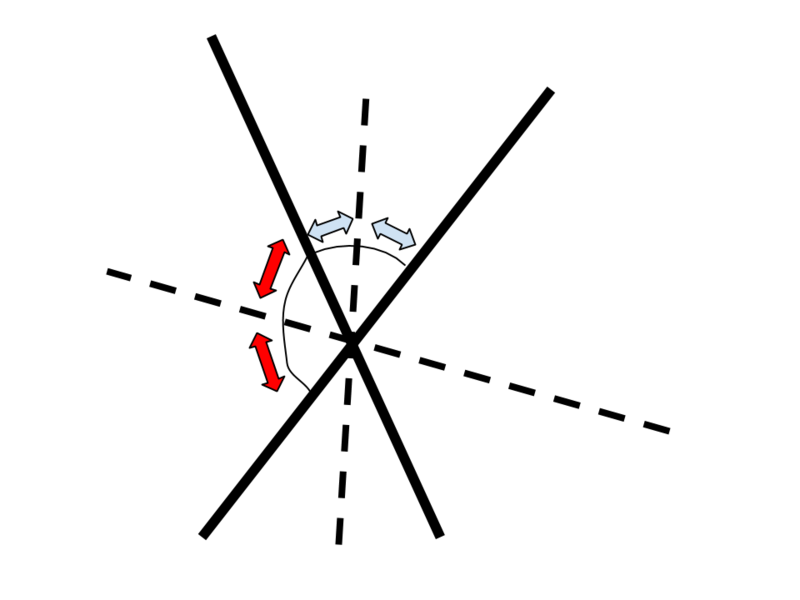
このように、条件を満たす点が存在する場所は直線になる
平行な場合は1本であり、そうでない場合は2本ある
このような直線を列挙し、その中から2本選んで交点を求め、その交点が入力で与えられた全ての線分と距離が等しいかを計算すれば良い
のだが、全て求めてしまうと最大 ( 2 * 100 * 100 ) ^ 2 本の直線が出来てしまうため良くない
しかし実際は全て列挙する必要はない
2本の交点はその他全ての候補となる線分上になければならないので
平行でない場合直線が2本現れることを考えても高々4本程度用意しておくだけで良い
答えとなる点を確定させるためには2本直線が必要で、平行でない場合は2本候補があるので2*2で4
ここで本数を制限する理由はオーダー削減なので(愚直にやると2*100*100の2乗)心配なら多めに10本余計にとっていても問題ない
あとはその答えの候補となる点について入力で与えられる全ての線分と距離を求め条件を満たしているものを数え上げ、1つならそれを出力、2つ以上あるならMany,0ならNoneと出力する
コード :
#include<bits/stdc++.h> #define REP(i,s,n) for(int i=s;i<n;i++) #define rep(i,n) REP(i,0,n) #define EPS (1e-6) #define equals(a,b) (fabs((a)-(b)) < EPS) #define COUNTER_CLOCKWISE 1 #define CLOCKWISE -1 #define ONLINE_BACK 2 #define ONLINE_FRONT -2 #define ON_SEGMENT 0 using namespace std; class Point{ public: double x,y; Point(double x = 0,double y = 0): x(x),y(y){} Point operator + (Point p){return Point(x+p.x,y+p.y);} Point operator - (Point p){return Point(x-p.x,y-p.y);} Point operator * (double a){return Point(a*x,a*y);} Point operator / (double a){return Point(x/a,y/a);} Point operator * (Point a){ return Point(x * a.x - y * a.y, x * a.y + y * a.x); } bool operator < (const Point& p) const{ return !equals(x,p.x)?x<p.x:(!equals(y,p.y)&&y<p.y); } bool operator == (const Point& p)const{ return fabs(x-p.x) < EPS && fabs(y-p.y) < EPS; } }; struct Segment{ Point p1,p2; int index; Segment(Point p1 = Point(),Point p2 = Point(),int index=-1):p1(p1),p2(p2),index(index){} bool operator < (const Segment& s) const { return ( p2 == s.p2 ) ? p1 < s.p1 : p2 < s.p2; } bool operator == (const Segment& s) const { return ( s.p1 == p1 && s.p2 == p2 ) || ( s.p1 == p2 && s.p2 == p1 ); } }; typedef Point Vector; typedef Segment Line; typedef vector<Point> Polygon; double dot(Point a,Point b){ return a.x*b.x + a.y*b.y; } double cross(Point a,Point b){ return a.x*b.y - a.y*b.x; } double norm(Point a){ return a.x*a.x+a.y*a.y; } double abs(Point a){ return sqrt(norm(a)); } Point rotate(Point a,double rad){ return Point(cos(rad)*a.x - sin(rad)*a.y,sin(rad)*a.x + cos(rad)*a.y); } double toRad(double agl){ return agl*M_PI/180.0; } double getArg(Point a,Point b,Point c){ double arg1 = atan2(b.y-a.y,b.x-a.x); double arg2 = atan2(c.y-b.y,c.x-b.x); double arg = fabs( arg1 - arg2 ); while( arg > M_PI ) arg -= 2.0 * M_PI; return fabs(arg); } int ccw(Point p0,Point p1,Point p2){ Point a = p1-p0; Point b = p2-p0; if(cross(a,b) > EPS)return COUNTER_CLOCKWISE; if(cross(a,b) < -EPS)return CLOCKWISE; if(dot(a,b) < -EPS)return ONLINE_BACK; if(norm(a) < norm(b))return ONLINE_FRONT; return ON_SEGMENT; } bool intersectLL(Line l, Line m) { return abs(cross(l.p2-l.p1, m.p2-m.p1)) > EPS || // non-parallel abs(cross(l.p2-l.p1, m.p1-l.p1)) < EPS; // same line } bool intersectLS(Line l, Line s) { return cross(l.p2-l.p1, s.p1-l.p1)* // s[0] is left of l cross(l.p2-l.p1, s.p2-l.p1) < EPS; // s[1] is right of l } bool intersectLP(Line l,Point p) { return abs(cross(l.p2-p, l.p1-p)) < EPS; } bool intersectSS(Line s, Line t) { return ccw(s.p1,s.p2,t.p1)*ccw(s.p1,s.p2,t.p2) <= 0 && ccw(t.p1,t.p2,s.p1)*ccw(t.p1,t.p2,s.p2) <= 0; } bool intersectSP(Line s, Point p) { return abs(s.p1-p)+abs(s.p2-p)-abs(s.p2-s.p1) < EPS; // triangle inequality } Point projection(Line l,Point p) { double t = dot(p-l.p1, l.p1-l.p2) / norm(l.p1-l.p2); return l.p1 + (l.p1-l.p2)*t; } Point reflection(Line l,Point p) { return p + (projection(l, p) - p) * 2; } double distanceLP(Line l, Point p) { return abs(p - projection(l, p)); } double distanceLL(Line l, Line m) { return intersectLL(l, m) ? 0 : distanceLP(l, m.p1); } double distanceLS(Line l, Line s) { if (intersectLS(l, s)) return 0; return min(distanceLP(l, s.p1), distanceLP(l, s.p2)); } double distanceSP(Line s, Point p) { Point r = projection(s, p); if (intersectSP(s, r)) return abs(r - p); return min(abs(s.p1 - p), abs(s.p2 - p)); } double distanceSS(Line s, Line t) { if (intersectSS(s, t)) return 0; return min(min(distanceSP(s, t.p1), distanceSP(s, t.p2)), min(distanceSP(t, s.p1), distanceSP(t, s.p2))); } Point crosspoint(Line l,Line m){ double A = cross(l.p2-l.p1,m.p2-m.p1); double B = cross(l.p2-l.p1,l.p2-m.p1); if(abs(A) < EPS && abs(B) < EPS){ vector<Point> vec; vec.push_back(l.p1),vec.push_back(l.p2),vec.push_back(m.p1),vec.push_back(m.p2); sort(vec.begin(),vec.end()); assert(vec[1] == vec[2]); return vec[1]; } if(abs(A) < EPS)assert(false); return m.p1 + (m.p2-m.p1)*(B/A); } double cross3p(Point p,Point q,Point r) { return (r.x-q.x) * (p.y -q.y) - (r.y - q.y) * (p.x - q.x); } bool collinear(Point p,Point q,Point r) { return fabs(cross3p(p,q,r)) < EPS; } bool ccwtest(Point p,Point q,Point r){ return cross3p(p,q,r) > 0; } bool onSegment(Point p,Point q,Point r){ return collinear(p,q,r) && equals(sqrt(pow(p.x-r.x,2)+pow(p.y-r.y,2)) + sqrt(pow(r.x-q.x,2) + pow(r.y-q.y,2) ),sqrt(pow(p.x-q.x,2)+pow(p.y-q.y,2)) ) ; } // ------------------ Line calcLine(Line line1,Line line2,Point p1,Point p2){ Point cp = crosspoint(line1,line2); int res = ccw(cp,p1,p2); Point base; if( res == COUNTER_CLOCKWISE ) base = p1; else base = p2; Point not_base = (base==p1)?p2:p1; double arg_a = (toRad(180.0)-getArg(base,cp,not_base)); Vector e = ( base - cp ) / abs( base - cp ); e = rotate(e,arg_a/2.0); Line tmp = Line(cp,cp+e*100); return tmp; } const string MANY = "Many"; const string NONE = "None"; void compute(vector<Line> &vec){ if( vec.size() <= 2 ) { cout << MANY << endl; return; } vector<Line> candidateLines; int n = vec.size(); rep(i,n) REP(j,i+1,n){ if( equals(cross(vec[i].p1-vec[i].p2,vec[j].p1-vec[j].p2),0.0) ) { Vector e = ( vec[i].p2 - vec[i].p1 ) / abs( vec[i].p2 - vec[i].p1 ); e = rotate(e,toRad(90)); Line line = Line(vec[i].p1,vec[i].p1+e*100); Point cp1 = crosspoint(line,vec[i]); Point cp2 = crosspoint(line,vec[j]); Point mp = ( cp1 + cp2 ) / 2.0; e = ( vec[i].p2 - vec[i].p1 ) / abs( vec[i].p2 - vec[i].p1 ); line = Line(mp,mp+e*100); line.index = candidateLines.size(); candidateLines.push_back(line); } else { Point cp = crosspoint(vec[i],vec[j]); Point I = ( vec[i].p1 == cp ) ? vec[i].p2 : vec[i].p1; Point J = ( vec[j].p1 == cp ) ? vec[j].p2 : vec[j].p1; Vector e1 = ( I - cp ) / abs( I - cp ); Vector e2 = ( J - cp ) / abs( J - cp ); Line tmp = calcLine(vec[i],vec[j],cp+e1*100,cp+e2*100); int Index = candidateLines.size(); tmp.index = Index; candidateLines.push_back(tmp); tmp = calcLine(vec[i],vec[j],cp+e1*100,cp-e2*100); tmp.index = Index; candidateLines.push_back(tmp); } if( candidateLines.size() >= 20 ) break; } vector<Point> candidatePoints; rep(i,candidateLines.size()) REP(j,i+1,candidateLines.size()) { Line line1 = candidateLines[i]; Line line2 = candidateLines[j]; if( equals(cross(line1.p1-line1.p2,line2.p1-line2.p2),0.0) ) continue; Point cp = crosspoint(line1,line2); candidatePoints.push_back(cp); } vector<Point> &v = candidatePoints; sort(v.begin(),v.end()); v.erase(unique(v.begin(),v.end()),v.end()); vector<Point> answer; rep(i,candidatePoints.size()){ Point p = candidatePoints[i]; double dist = -1; bool success = true; rep(j,vec.size()){ double tmp = distanceLP(vec[j],p); if( equals(dist,-1) ) dist = tmp; else if( !equals(dist,tmp) ) { success = false; break; } } if( success ) answer.push_back(p); if( answer.size() >= 2 ) break; } if( answer.size() == 1 ) printf("%.10f %.10f\n",answer[0].x,answer[0].y); else if( answer.empty() ) cout << NONE << endl; else cout << MANY << endl; } int main(){ int n; while( cin >> n, n ){ vector<Line> vec(n); rep(i,n) cin >> vec[i].p1.x >> vec[i].p1.y >> vec[i].p2.x >> vec[i].p2.y; compute(vec); } return 0; }