土下座しながら探索中

主に競技プログラミング

ACM-ICPC 2016 国内予選　参加記

ACM-ICPC 国内予選

最後の国内予選なので参加記を残そうかと
チームは私と後輩Sと後輩Tです。（イニシャルだけだと去年と同じだけど後輩Tは去年とは別の人
[追記]後輩Tではなく後輩Mでした、後輩Mさんごめんなさい　

リハーサル

後輩Sは2,3限に授業があるため不参加
後輩Mとともに会場準備とプリンタの設定を行う
お菓子とMAXコーヒーとレッドブルとT島屋で買った100g1670円のブルーマウンテンを挽いていれたコーヒーを飲む
自己紹介を書いたりする
TwitterのTLを眺めながら後輩らの精神状況が不安定であることを確認する
コンテスト中のチームの動きを確認する
コンテスト開始を待つ

コンテスト

A問題

ソートするだけっぽい
絶対AでWAを出したくないので後輩Sに「本当にそれだけ？」とn回確認した
「条件どうこういってたけど、それはなんだったの？」「本当にそれだけ？？」「えっ」
コードを書く、サンプルは通る
まぁ投げてみる => AC
良い感じ
１完

B問題

後輩Mから概要を聞く
全探索で良いみたい
書く=>サンプルが合わない
バグとりを二人でする
入力に現れる立候補者の他に１名立候補者を入れる必要があることが発覚
入れる、それに合わせてループを修正
サンプルは通る
まぁ投げてみる => AC
ちょっとつまったけど良い感じ
２完

C問題

後輩Sから概要を聞く
「エラトステネスの篩です、以上」
この説明から概要がつかめなかったで問題文に目を通す
なるほど、エラトステネスの篩っぽいものを書けば良いようだ
書く=>無限ループ
悲しい気持ちになりつつもデバッグ
無限ループは止まった
でもサンプルは合わない
後輩Sと色々話しながらバグを探す、修正
サンプルは通る
まぁ投げてみる => AC
プログラムを実行してからアウトプットが終わるまで２、３分かかっていて辛い感じだったけどまぁ通ったし良い感じ
３完

D問題

概要を聞く前に解けそうか聞いてみる
二人から分からないと返事が返ってきて悲しい気持ちになる
概要を聞く
「あれ、超見たことあるこれ絶対区間DPだゾ（適当」

という発言したはいいもののはっきりとした方針が浮かんでこない
とりあえず後ろの問題に一通り目を通す
Fぱっとみ簡単そう、でもさすがにDのほうが楽そう
Dをやることにする

冷静に考えて、bool memo[L][R]みたいな感じで全て消すことのできる区間を列挙してあとは
dp[i]:=iまでで作れる最大値　みたいなDPすれば良い

書く=>めっちゃバグる＝＞辛い気持ちになりつつ後輩Mと共にデバッグをする
暗黒時代の幕開け
後輩Mが正しい方針を示すもそれとは全く違う実装をして時間を無駄にする
頑張る
暗黒時代が終わる
サンプルは通る
まぁ投げてみる => AC
スコアボードを確認するとまぁ良いでしょみたいな順位にいたので良い感じ
４完

とりあえず残りの問題のどれに挑戦するか話し合う
E ... 一番ダメそう
F ... 一番いけそう
G ... 自分には無理そう、後輩Sは挑戦したいらしい
H ... 二番目にいけそう

というわけで自分はFを書き、
後輩SはGを考え、
後輩MはHを考えることに

F問題

内包関係をグラフにするとそれは木になるし、だったらあとは木の同型判定でしょ
まだ１時間以上あるしいける木がする
実装開始と共に暗黒時代が幕を開ける
残り１時間 => まだまだ書くことがある
残り30分 => まだまだまだ書くことがある
残り10分 => まだまだまだまだ書くことがある、なんだこれは

コンテストが終わった
実装力が足りていない（もしくはコーダーが足りていない

感想

アジアに向けてコーダーを育てようと決意

SRM 692 Div1 easy : HardProof

SRM 強連結成分分解 グラフ 橋

問題概要 :

任意の２点間に辺があるような重み付き有向グラフが隣接行列Dとして与えられる

このグラフはn個の頂点から成り、各頂点には0から順にn-1まで番号が割り振られている

全ての頂点を少なくとも１回以上訪れるような閉路について考えたとき、

この閉路に含まれる辺の重みの最大値と最小値の差の最小値を求めよ

解法 :

強連結成分分解 + 二分探索で解いた

まず、閉路中に存在する辺の重みの最大値と最小値を決める

ただし愚直に最大値と最小値を決めてしまうと全ての辺の重みが異なる場合にTLEする

( 最大値、最小値の取りうる数はそれぞれ2500なので総当たりすると2500 * 2500, その後の処理に2500かかるので 2500^3 で TLE する　その後の処理をlogくらいに抑えれればTLEしないけど)

そこで、最小値だけを総当たりで決める

最小値が決まったとき、最小値以上の最大値の最小値は二分探索により求めることができる

このとき、与えられたグラフの中から辺の重みが最小値未満もしくは最大値より大きいものを除いたグラフについて考える

このグラフ中に、全ての頂点を少なくとも１回以上訪れるような閉路が存在すれば良い

ここでは既に余計な辺を削除してあるので、このグラフ中に平路が存在するかどうかを判定すれば良い

これはグラフ中に橋が存在するかどうかで判断できる

( 橋とは？ 参考 : http://hos.ac/slides/20110504_graph.pdf

橋 : グラフ中に存在する辺のうち、それを取るとグラフの連結成分数が増えるようなもののこと)

今回グラフは有向グラフなので、強連結成分の数が１つかどうかで判断できる

強連結成分の数が２以上なら、異なる２つの強連結成分同士を結ぶような辺が橋になるからである

V,Eをそれぞれグラフの頂点集合、辺集合とすると計算量は
閉路中の辺の重みの最小値を総当たりするので |V| = 2500
二分探索で最大値を決定するので log2(|V|) = log2(2500) ≒11.287712379549449
強連結成分分解 |V| + |E| = 50 + 2500
O( |V| * log(|V|) * (|V|+|E|) )
最悪ケースでは 2500 * log2(2500) * 2550 ≒ 70548202.37218405となる
10^8以下なので十分１秒以内に終わる

コード :

#include<bits/stdc++.h>

#define REP(i,s,n) for(int i=s;i<n;i++)
#define rep(i,n) REP(i,0,n)
#define EPS 1e-10
#define equals(a,b) (fabs((a)-(b)) < EPS)

using namespace std;

const int IINF = INT_MAX;

int V;
int mat[51][51];
bool visited[51];

class HardProof {
public:

  int lower, upper;

  vector<vector<int> > G,rG;
  vector<bool> used;
  vector<int> cmp,vs;

  void add_edge(int s,int t){
    G[s].push_back(t);
    rG[t].push_back(s);
  }

  void dfs(int v){
    used[v] = true;
    for(int i=0;i<(int)G[v].size();i++) if( !used[G[v][i]] ) dfs(G[v][i]);
    vs.push_back(v);
  }

  void rdfs(int v,int k){
    used[v] = true;
    cmp[v] = k;
    for(int i=0;i<(int)rG[v].size();i++) if( !used[rG[v][i]] ) rdfs(rG[v][i],k);
  }

  int scc(){
    rep(i,V) used[i] = false;
    vs.clear();
    rep(v,V) if( !used[v] ) dfs(v);
    rep(i,V) used[i] = false;
    int k = 0;
    for(int i=vs.size()-1;i>=0;i--) if( !used[vs[i]] ) rdfs(vs[i],k++);
    return k;
  }

  bool check() {
    if( lower > upper ) return false;
    G.clear(), rG.clear(), cmp.clear(), used.clear();
    G.resize(V,vector<int>()), rG.resize(V,vector<int>()),cmp.resize(V), used.resize(V);
    rep(i,V) {
      rep(j,V) if( i != j && ( lower <= mat[i][j] && mat[i][j] <= upper ) ) {
	add_edge(i,j);
      }
    }
    return scc() == 1;
  }

  int minimumCost(vector <int> D) {
    V = sqrt((int)D.size());
    if( V == 1 ) return 0;
    rep(i,V) rep(j,V) mat[i][j] = D[i*V+j];
    vector<int> lowers;
    rep(i,V) rep(j,V) lowers.push_back(mat[i][j]);
    sort(lowers.begin(),lowers.end());
    lowers.erase(unique(lowers.begin(),lowers.end()),lowers.end());
    int mini = IINF;
    rep(i,(int)lowers.size()) {
      lower = lowers[i];
      int L = 0, R = ((int)lowers.size());
      while( L + 1 < R ) {
	int M = ( L + R ) / 2;
	upper = lowers[M];
	if( check() ) {
	  R = M;
	  mini = min(mini,upper-lower);
	} else {
	  L = M;
	}
      }
    }
    return mini;
  }
};

SRM 691 Div1 easy : Sunnygraphs

SRM グラフ

問題概要 :
n個の頂点とn本の無向辺があり、頂点は0からn-1まで番号が割り振られている
また、辺は頂点iから頂点a[i]に向けて貼られている ( ただし、i != a[i] )

このグラフに対して次の処理を行う
1. 新たな頂点 n を追加する
2. 0からn-1までの頂点集合から任意の部分集合Mを選ぶ
3. Mに属する頂点 i について、辺(i,a[i])をグラフから取り除く
4. Mに属する頂点 i について、辺(i,n)をグラフに追加する

この処理を行ったあと、0から1へのパスが存在するようなMの選び方は何通り存在するか？

解法 :
グラフの取りうる状態について考える
グラフの状態は初期状態で0と1の間にパスが存在するかしないかで分けられるため、それぞれについて考えていく
今後、説明上どの頂点からどの頂点に向けて辺が貼られているのかを明らかにするためグラフの辺は有向辺として書くが実際は無向辺であるので注意すること

まず、0と1の間にパスが存在しない場合のグラフは次のようになる
f:id:tei3344:20160531024608j:plain
このグラフは0から到達可能な頂点集合(上の図では頂点0,2)と1から到達可能な頂点集合(上の図では頂点1,3)、それ以外の頂点集合(上の図では頂点4,5)から成る
それ以外の頂点集合は空集合でも良い
0と1の間にパスをつくるためには、
0から到達可能な頂点集合から少なくとも1つ、
1から到達可能な頂点集合から少なくとも1つの頂点をMとして選ぶ必要がある
f:id:tei3344:20160531025416p:plain
0と1から到達可能な頂点集合からそれぞれ少なくとも1つの頂点をMとして選んだのであれば、
それ以外の頂点集合はMに追加してもしなくてもどちらでもよい
これより、0と1の間にパスが存在しない場合の答えは (2^(0から到達可能な頂点集合の大きさ)-1) * (2^(1から到達可能な頂点集合の大きさ)-1) * (2^(それ以外の頂点集合の大きさ))で求めることができる
答えの式中にある-1は1つも頂点を選ばない場合を取り除くためのものである

次に、0と1の間にパスが存在する場合のグラフについて考える
このときグラフは次のようになる
f:id:tei3344:20160531031045p:plain
このグラフの頂点集合は次のように分類することができる
0と1のそれぞれから探索を開始したとき、

\* 0からのみ到達可能な頂点集合 ( 上の図では頂点0,2 )
\* 1からのみ到達可能な頂点集合 ( 上の図では頂点1,4)
\* 両方から到達可能な頂点集合 ( 上の図では頂点3,5,6)
\* 両方から到達不可能な頂点集合( 上の図では頂点7,8 )
このグラフはすでに0と1の間にパスが存在するため、そのパスを壊さないような頂点Mの選び方が答えとなる

パスを壊さないような頂点の選び方は次の５通りである
\* 0からのみ到達可能な頂点集合と1からのみ到達可能な頂点集合から少なくとも1つは頂点をMとして選ぶ
f:id:tei3344:20160531031733p:plain
このとき、両方から到達可能、到達不可能な頂点集合からは頂点をMとして選んでも選ばなくても良い
そのため、このときのMの選び方は(2^(0から到達可能な頂点集合の大きさ)-1) * (2^(1から到達可能な頂点集合の大きさ)-1) * (2^(両方から到達可能な頂点集合の大きさ)) * (2^(両方から到達不可能な頂点集合の大きさ))となる


\* 0からのみ到達可能な頂点集合から少なくとも1つは頂点をMとして選ぶ, 1からのみ到達可能な頂点集合からは1つも選ばない
f:id:tei3344:20160531032412j:plain
これだけでは0と1の間にパスができないため、両方から到達可能な頂点集合から少なくとも1つはMとして選ぶ必要がある
そのため、このときのMの選び方は(2^(0から到達可能な頂点集合の大きさ)-1) * (2^(両方から到達可能な頂点集合の大きさ)-1) * (2^(両方から到達不可能な頂点集合の大きさ))となる

\* 1からのみ到達可能な頂点集合から少なくとも1つは頂点をMとして選ぶ, 0からのみ到達可能な頂点集合からは1つも選ばない
f:id:tei3344:20160531032728j:plain
これだけでは0と1の間にパスができないため、両方から到達可能な頂点集合から少なくとも1つはMとして選ぶ必要がある
そのため、このときのMの選び方は(2^(1から到達可能な頂点集合の大きさ)-1) * (2^(両方から到達可能な頂点集合の大きさ)-1) * (2^(両方から到達不可能な頂点集合の大きさ))となる

\* 0からのみ到達可能な頂点集合と1からのみ到達可能な頂点集合からは頂点を１つも選ばない、両方から到達可能な頂点集合から少なくとも1つはMとして選ぶ
f:id:tei3344:20160531032923j:plain
0からのみ到達可能な頂点集合と1からのみ到達可能な頂点集合からは1つも頂点をMとして選んでいないため、0と1の間にはパスが残ったままである
そのため、このときのMの選び方は(2^(両方から到達可能な頂点集合の大きさ)-1) * (2^(両方から到達不可能な頂点集合の大きさ))となる

\* 両方から到達不可能な頂点集合からのみ頂点をMとして選ぶ
f:id:tei3344:20160531033302j:plain
このときのMの選び方は(2^(両方から到達不可能な頂点集合の大きさ))となる

これら５通りの選び方の総和が答えとなる

コード:

#include<bits/stdc++.h>

#define REP(i,s,n) for(int i=s;i<n;i++)
#define rep(i,n) REP(i,0,n)
#define EPS 1e-10
#define equals(a,b) (fabs((a)-(b)) < EPS)

using namespace std;

const int IINF = INT_MAX;
typedef long long ll;

vector<int> G[100],checkG[100];

typedef pair<int,int> ii;

inline void fix(ii &v) { if(v.first > v.second) swap(v.first,v.second); }

void dfs(int cur,map<ii,ll> &mp) {
  rep(i,(int)G[cur].size()) {
    ii edge = ii(cur,G[cur][i]);
    if( mp.count(edge) ) continue;
    ++mp[edge];
    dfs(G[cur][i],mp);
  }
}

bool used[100];
bool checkDFS(int cur) {
  if( cur == 1 ) return true;
  bool res = false;
  rep(i,(int)checkG[cur].size()) {
    int &next = checkG[cur][i];
    if( used[next] ) continue;
    used[next] = true;
    res |= checkDFS(next);
  }
  return res;
}

class Sunnygraphs {
public:
  long long count(vector <int> a) {
    rep(i,(int)a.size()) {
      G[i].push_back(a[i]);
      checkG[i].push_back(a[i]);
      checkG[a[i]].push_back(i);
    }
    map<ii,ll> counter0,counter1;
    dfs(0,counter0);    
    dfs(1,counter1);
    long long zero = (long long)counter0.size();
    long long one  = (long long)counter1.size();
    long long otherwise = (int)a.size();
    if( !checkDFS(0) ) {
      otherwise -= ( zero + one );
      return ((1LL<<zero)-1LL) * ((1LL<<one)-1LL) * (1LL<<otherwise);
    }
    long long common = 0, answer = 0;
    for(map<ii,ll>::iterator it=counter0.begin();it!=counter0.end();it++) {
      ii v = it->first;
      if( counter1.count(v) ) {
	++common;
      }
    }
    zero -= common, one -= common;
    otherwise -= ( zero + one + common);
    if( zero && one ) {
      answer += ( ((1LL<<zero)-1LL) * ((1LL<<one)-1LL) * (1LL<<common) * (1LL<<otherwise) );
    }
    if( zero ) {
      answer += ( ((1LL<<common)-1LL) * ((1LL<<(zero))-1LL) * (1LL<<otherwise) );
    }
    if( one ) {
      answer += ( ((1LL<<common)-1LL) * ((1LL<<(one))-1LL) * (1LL<<otherwise) );
    }
    if( common ) {
      answer += ((1LL<<common)-1LL) * (1LL<<otherwise);
    }
    answer += (1LL<<otherwise);
    return answer;

  }
};

SRM 688 Div1 easy : ParenthesesDiv1Easy

SRM Bracket

問題概要 :
'('と')'からなる文字列sが与えられる
この文字列に対して次の処理(1,2を連続で)を行うことができる
1. ２つの整数l,r (l<=r)について、 s[l]からs[r]までを反転させる
例 s = "((()", l = 1, r = 3 => s = "((("
2. s[l]からs[r]までの各文字に対して、'('なら')'に、')'なら'('に変更する
例 s = "((()", l = 1, r = 3 => s = "(())"

このとき、文字列sを正しい括弧の対応付けにするまでに必要な処理の内容を出力せよ
ただし、処理は高々10回までとする
正しい括弧の対応付けにできない場合は-1を返すこと
※正しい括弧の例 (), (()), ((()))()(()())

解法 :
処理にどのような特徴があるのか考える
この処理は指定した範囲の部分文字列を単純に反転した後にその中の括弧も反転させる、というもの
そのため、指定した範囲内に存在する正しい括弧は処理を行った後も正しい括弧のままである
例えば、s = "()(", l = 0, r = 3 の処理結果は s = ")()" となる
今後処理をする際に正しい括弧を破壊する意味はないため、正しい括弧は取り除いて考えることができる
例えば、s = "()()()))((((())"　は s = ")(((" として考えることができる
正しい括弧を全て取り除いて考えたとき、sのとりうる状態は以下の３通りしか存在しない

1. 全て '('
2. 全て ')'
3. ')' が１つ以上続いた後に '(' が１つ以上続く 例 s = "))))((("

これ以外だと正しい括弧が残っていることになる

結局この３通りだけしかないのであれば、

1. の場合は取り除かれなかった'('の後半分を')'に変換すれば良い
2. の場合は取り除かれなかった')'の前半分を'('に変換すれば良い
3. の場合は取り除かれなかった'('を全て')'に変換 or ')' を全て '(' に変換すると1.か2.の状態になるため上の通りに処理すれば良い

ということになる

例

     0123456789012345
s = "()()())()((((())"

まず、正しい括弧を取り除く

s = "()()())()( ( (( ())"

     6901
s = ")((("

次に、s を ')' か '(' のどちからのみからなるように変換する
どちらでも良いので今回は ')' だけからなるように変換する

s = ")(((", l = 9, r = 11

s = "))))"

最後に、')'の前半分を'('に変換して正しい括弧の対応付けにする

s = "))))"

s = "(())"

コード :

#define REP(i,s,n) for(int i=s;i<n;i++)
#define rep(i,n) REP(i,0,n)

using namespace std;

typedef long long ll;
typedef pair<char,int> ci;
const int IINF = INT_MAX;


class ParenthesesDiv1Easy {
public:

  deque<ci> calcDeq(string s) {
    deque<ci> deq;
    rep(i,(int)s.size()) {
      if( s[i] == '(' ) {
        deq.push_back(ci('(',i));
      } else {
        if( (int)deq.size() && deq.back().first == '(' ) deq.pop_back();
        else deq.push_back(ci(')',i));
      }
    }
    return deq;
  }

  string flip(string s,int l,int r) {
    reverse(s.begin()+l,s.begin()+r+1);
    for(int i=l;i<=r;++i) {
      if( s[i] == '(' ) s[i] = ')';
      else              s[i] = '(';
    }
    return s;
  }

  vector <int> correct( string s ) {
    int n = s.size();
    if( n & 1 ) return vector<int>(1,-1);
    deque<ci> deq = calcDeq(s);
    // ()()())()((((()) 
    bool hasL = false, hasR = false;
    int sp = IINF;
    rep(i,(int)deq.size()) {
      if( deq[i].first == '(' ) hasL = true, sp = min(sp,i);
      else                      hasR = true;
    }

    vector<int> ret;
    int len = deq.size();
    if( hasL && hasR ){
      ret.push_back(deq[sp].second);
      ret.push_back(n-1);
      s = flip(s,deq[sp].second,n-1);
      deq = calcDeq(s);
      hasL = false;
    }
    
    if( hasL ) {
      ret.push_back(deq[len/2].second);
      ret.push_back(n-1);
    } else if( hasR ) {
      ret.push_back(0);
      ret.push_back(deq[(int)(len/2)-1].second);
    }
    return ret;
  }
};

SRM 682 Div1 easy : SmilesTheFriendshipUnicorn

SRM Ad-Hoc

問題概要 :
N人の人がいて、それらの人は0からN-1まで順に番号が割り振られている
これらの人の間には友好関係があり、これは２つの整数で表される
友好関係は2つの配列A,Bとして表されA[i]番の人とB[i]番の人は友達である
A[i] != B[i]
これらの友好関係は無向グラフとして表すことができる
このとき、任意の２頂点間には必ずパスが存在する
このグラフ内に長さが４のパスが存在するか、YESかNOで答えよ
つまり、5つの異なる頂点a,b,c,d,eについて、
aとb,bとc,cとd,dとeに辺が存在する

解法 :
無向グラフ内から下の図のような部分が存在するかを判定したい
f:id:tei3344:20160223133648p:plain
このとき、
f:id:tei3344:20160223133744p:plain
すぐ上の図の赤い枠で囲まれた辺をループで愚直に決めてしまう
赤い枠で囲まれた辺は２本しかないので、2000 * 2000 で４つの頂点からなる長さ３のパスを求めることができる
残り１つの頂点は長さ３のパスの両端点について、次数からO(1)で計算できる

まず２つの辺から長さ３のパスを計算する
f:id:tei3344:20160223134116p:plain
以下の４通りのパスが存在する
f:id:tei3344:20160223134203j:plain
f:id:tei3344:20160223134217j:plain
f:id:tei3344:20160223134233j:plain
f:id:tei3344:20160223134252j:plain

この各４通りのパスについて、端点に１つ頂点が追加できれば求めたいパスになる
これは次数からO(1)で計算できる
先ほどの１つめの例で考えると、
f:id:tei3344:20160223134506j:plain
2番か4番の頂点から5番に辺があれば良い
2番の頂点に注目したとき、5番の頂点というのは1,3,4番の頂点でなければどれでもよい
つまり、２番の頂点の次数をdegとしたとき、
2-1に辺は必ず存在するので --deg
2-3に辺が存在するなら --deg
2-4に辺が存在するなら --deg
この結果が1以上であれば、１でも３でも４でもない頂点と２は繋がっている
これを５とすればよい

コード :

#include<bits/stdc++.h>

#define REP(i,s,n) for(int i=s;i<n;i++)
#define rep(i,n) REP(i,0,n)

using namespace std;

typedef long long ll;
const int IINF = INT_MAX;
const string kzy = "Yay!";
const string KT  = ":(";

struct Edge {
  int s,t;
  bool operator < (const Edge& e) const {
    if( s != e.s ) return s < e.s;
    return t < e.t;
  }
};

bool rel[2010][2010];
vector<int> G[2010];

class SmilesTheFriendshipUnicorn {
public:

  bool check(Edge e1,Edge e2,bool sp1,bool sp2) {
    int p1 = -1, p2 = -1;
    int rp1 = -1, rp2 = -1;
    if( sp1 ) p1 = e1.t, rp1 = e1.s;
    else      p1 = e1.s, rp1 = e1.t;
    if( sp2 ) p2 = e2.t, rp2 = e2.s;
    else      p2 = e2.s, rp2 = e2.t;
    if( !rel[p1][p2] ) return false;
    
    int deg1 = (int)G[rp1].size();
    int deg2 = (int)G[rp2].size();
    
    //
    --deg1;
    if( rel[rp1][p2] ) --deg1;
    if( rel[rp1][rp2] ) --deg1;
    if( deg1 >= 1 ) return true;
    
    //
    --deg2;
    if( rel[rp2][p1] ) --deg2;
    if( rel[rp2][rp1] ) --deg2;
    if( deg2 >= 1 ) return true;
    
    return false;
  }

   string hasFriendshipChain( int N, vector <int> A, vector <int> B ) {
     N = N;
     vector<Edge> vec;
     rep(i,(int)A.size()) {
       vec.push_back((Edge){A[i],B[i]});
       G[A[i]].push_back(B[i]);
       G[B[i]].push_back(A[i]);
       rel[A[i]][B[i]] = rel[B[i]][A[i]] = true;
     }
     rep(i,(int)vec.size()) {
       Edge &e1 = vec[i];
       rep(j,(int)vec.size()) {
         Edge &e2 = vec[j];
         if( e1.s == e2.s || e1.s == e2.t ) continue;
         if( e1.t == e2.s || e1.t == e2.t ) continue;
         if( check(e1,e2,0,0) ) return kzy;
         if( check(e1,e2,0,1) ) return kzy;
         if( check(e1,e2,1,0) ) return kzy;
         if( check(e1,e2,1,1) ) return kzy;
       }
     }
     
     return KT;
   }
};

Codeforces AIM Tech Round (Div. 2) C : Graph and String

Adhoc Coedforces

問題リンク :
http://codeforces.com/contest/624/problem/C

問題概要 :
長さnの{'a','b','c'}で構成されている文字列が存在した
これを次の手順でグラフに変換した
1. n個のノードを作成、各ノードに１から順に番号を割り振る
2. 異なる２つのノード番号i,jについて、文字列のi番とj番が一致または隣接していればノードiとノードjに辺を張る
ここで、隣接とはa-b,b-cのことをであり、a-cは隣接とは言わない
この手順でグラフを作成したあと、文字列を消した

グラフが与えられるので、上記の手順にしたがった場合与えられたグラフになるような文字列を出力せよ
複数存在するならどれか１つでよい
存在しない場合はNoと出力せよ

解法:
ノードがちょうど1つしか存在しない場合、明らかに答えとなる文字列は存在する
'a'か'b'か'c'である
どれか好きなのを出力すると良い

ノードがちょうど２つ存在する場合、これも必ず答えとなる文字列は存在する
その２つのノード間に辺があるなら、'a'-'b'か'b'-'c'か'a'-'a','b'-'b','c'-'c'のいずれかを出力するとよい
辺がないなら隣接していないので'a'-'c'が答えとなる

ノードが３つ以上存在する場合、次のような部分をグラフから探す
f:id:tei3344:20160205044801p:plain
このような部分が存在しないなら、存在する頂点は全て完全グラフの一部となっているはずである
つまり完全グラフが何個か存在することになる
完全グラフが１つしかないなら、明らかに答えは存在する（全て同じ文字とか）
完全グラフが２つなら、0の完全グラフと２の完全グラフが存在する
それ以上存在するなら答えはない　０と２で２つまでなら完全グラフをつくれるが、もう１つ追加しからそれが０の完全グラフであれ、１であれ、２であれ、どれでも最初の２つの完全グラフとくっついてしまう

上の図のような、三角形の一辺を抜いた部分が存在するなら、
その図にある０番のノードは'b'であり、１番のノードと２番のノードはどちらかが'a'でもう片方が'c'である
このとき、1番のノードに辺がつながっているノードは１に割り当てられた英小文字（'a'か'c')か０に割り当てられた英小文字('b')と一致するはずである
同様に２番のノードに辺がつながっているノードは２番に割り当てられた英小文字('a'か'c')か０番に割り当てられた英小文字（'b')と一致するはず
f:id:tei3344:20160205050548p:plain
これらを集合にしたとき（上の図でいう、点線内のノード番号を集合としたとき）
両方の集合に属することができるのは'b'しかないので、それらのノードには'b'を割り当てる
そうでないものは、どちらかを'a'の集合、もう片方は'c'の集合と決めて（どっちでも良いので）割り当てる
あとは頂点集合全体を見て、'a','b','c'のいずれも割り当てられていないものがあればNoと出力し、
そうでないなら答えとなる文字列を生成して、一応入力のグラフができるかチェックして大丈夫ならそれを出力する

コード:

#include<bits/stdc++.h>

#define REP(i,s,n) for(int i=s;i<n;i++)
#define rep(i,n) REP(i,0,n)

using namespace std;

typedef long long ll;
const int IINF = INT_MAX;
const ll LLINF = LLONG_MAX;
const int MAX = 600;

const string YES = "Yes";
const string NO = "No";
typedef pair<int,int> ii;

int V,E;
vector<int> G[MAX];
bool mat[MAX][MAX];
bool vmat[MAX][MAX];
vector<ii> edges;
char c[MAX];

void dfs(int cur,set<int> &S) {
  rep(i,(int)G[cur].size()) {
    int next = G[cur][i];
    if( S.count(next) ) continue;
    S.insert(next);
    dfs(next,S);
  }
}

int compute() {

  if( V == 1 ) {
    cout << YES << endl;
    return puts("b");
  }
  if( (int)((V*(V-1))/2) == E ) {
    cout << YES << endl;
    return puts(string(V,'b').c_str());
  }

  rep(i,V) c[i] = '$';
  set<int> S0;
  set<int> S2;
  rep(i,(int)edges.size()) {
    int s = edges[i].first;
    int t = edges[i].second;
    rep(p,V) {
      if( s == p || t == p ) continue;
      if( !mat[p][t] && !mat[p][s] ) continue;
      if( mat[p][t] && mat[p][s] ) continue;
      int ID0,ID1 , ID2;
      if( mat[p][s] ) {
	ID0 = t, ID1 = s, ID2 = p;
      } else {
	ID0 = s, ID1 = t, ID2 = p;
      }

      S0.insert(ID1);
      S0.insert(ID0);
      S2.insert(ID1);
      S2.insert(ID2);
      rep(k,V) {
	if( k == s || k == t || k == p ) continue;
	if( mat[ID0][k] ) S0.insert(k);
	if( mat[ID2][k] ) S2.insert(k);
      }
      goto Skip;
    }
  }
 Skip:;

  if( S0.empty() ) {
    S0.insert(0);
    dfs(0,S0);
    rep(i,V) if( !S0.count(i) ) {
      S2.insert(i);
      dfs(i,S2);
      break;
    }
    for(set<int>::iterator it=S0.begin();it!=S0.end();it++) {
      c[*it] = 'a';
    }

    for(set<int>::iterator it=S2.begin();it!=S2.end();it++) {
      c[*it] = 'c';
    }
    rep(i,V) if( c[i] == '$' ) {
      return puts(NO.c_str());
    }
    puts(YES.c_str());
    rep(i,V) {
      printf("%c",c[i]);
    } puts("");
    return 0;
  }

  rep(i,V) {
    if( S0.count(i) && S2.count(i) ) {
      c[i] = 'b';
    } else if( S0.count(i) ) {
      c[i] = 'a';
    } else if( S2.count(i) ) {
      c[i] = 'c';
    }
  }
  /*
  cout << "S0::" << endl;
  for(set<int>::iterator it=S0.begin();it!=S0.end();it++) {
    cout << *it << " ";
  } puts("");

  cout << "S2::" << endl;
  for(set<int>::iterator it=S2.begin();it!=S2.end();it++) {
    cout << *it << " ";
  } puts("");
  */
  string answer = "";
  rep(i,V) {
    if( c[i] == '$' ) {
      return puts(NO.c_str());
    }
    answer += string(1,c[i]);
  }

  
  rep(i,V) REP(j,i+1,V) {
    int v1 = c[i] - 'a';
    int v2 = c[j] - 'a';
    if( abs(v1-v2) <= 1 ) {
      vmat[i][j] = vmat[j][i] = true;
    }
  }

  rep(i,V) rep(j,V) if( mat[i][j] != vmat[i][j] ) {
    return puts(NO.c_str());
  }
  puts(YES.c_str());
  return puts(answer.c_str());
}

int main(){
  scanf("%d %d",&V,&E);
  int s,t;
  rep(i,E) {
    scanf(" %d %d",&s,&t);
    --s, --t;
    mat[s][t] = mat[t][s] = true;
    G[s].push_back(t);
    G[t].push_back(s);
    if( s > t ) swap(s,t);
    edges.push_back(ii(s,t));
  }
  compute();
  return 0;
}

Typical DP Contest J : ボール

典型DPコンテスト 動的計画法

問題リンク :
J: ボール - Typical DP Contest | AtCoder

問題概要：略

解法：
期待値苦手すぎて謎だったので以下の解説記事を参考にしました
Typical DP Contest J - ボール - Lilliput Steps

ビットDP (orメモ化再帰)
まだ倒れていないものがある場所に対応するビットを1にしておきます
dp[bit] := 倒れていないものの状態がbitで、ここからすべて倒すまでに必要なボールを投げる回数の期待値

状態bitからボールを投げるとき、次に投げるボールを落とす位置をすべて試してみて、その中で最小の期待値をdp[bit]にいれる

状態bitから全て倒すために必要な期待値は、狙った場所をxとしたとき
dp[bit] = dp[bit&~(1<< ( x - 1 ) ) ] / 3 + dp[bit&~ ( 1 << x ) ] / 3 + dp[bit&~(1<< ( x + 1 ) ) ] / 3
このxを全てためしてみてその最小値をdp[bit]にいれる
ただし、x,x-1,x+1のうち、すでに倒した場所orそもそもない場所に落ちたときはdp[bit]が左辺に残ることになる
なので、そのときはその部分を左辺に以降すること

コード1(メモ化再帰):

#include<bits/stdc++.h>

#define REP(i,s,n) for(int i=s;i<n;i++)
#define rep(i,n) REP(i,0,n)
#define EPS (1e-9)
#define equals(a,b) (fabs((a)-(b))<EPS)

using namespace std;

const double DINF = DBL_MAX;

int n,bitmask,x[20];
double memo[1<<20];

double dfs(int state) {
  if( !state ) return 0;
  if( !equals(memo[state],DINF) ) return memo[state];
  REP(i,1,17) {
    double ex = 1;
    double same = 0;
    REP(dx,-1,2) {
      int p = i + dx; 
      int nstate = state;
      nstate = state & ~(1<<p);
      if( state == nstate ) ++same;
      else {
	ex += dfs(nstate) / 3.0;
      }
    }
    ex = ( ex * 3.0 ) / ( 3.0 - same );
    memo[state] = min(memo[state],ex);
  }
  return memo[state];
}

int main() {
  cin >> n;
  rep(i,n) {
    cin >> x[i];
    ++x[i];
    bitmask |= (1<<x[i]);
  }
  rep(i,(1<<18)) memo[i] = DINF;
  printf("%.10f\n",dfs(bitmask));
  return 0;
}

コード2(ビットDP）:

#include<bits/stdc++.h>

#define REP(i,s,n) for(int i=s;i<n;i++)
#define rep(i,n) REP(i,0,n)
#define EPS (1e-8)
#define equals(a,b) (fabs((a)-(b))<EPS)

using namespace std;

const double DINF = DBL_MAX;

int n,x[20],bitmask;
double dp[1<<20];

int main() {
  cin >> n;
  rep(i,n) {
    cin >> x[i];
    ++x[i];
    bitmask |= (1<<x[i]);
  }
  rep(i,(1<<20)) dp[i] = DINF;
  dp[0] = 0;
  for(int state=1;state<=bitmask;state++) {
    if( state & ~bitmask ) continue;
    double mini = DINF;
    for(int p=1;p<=16;p++) {
      double ex = 0;
      double same = 0;
      bool fail = false;
      for(int dx=-1;dx<=1;dx++) {
	int np = p + dx;
	int next_state = state;
	if( (bitmask>>np) & 1 ) next_state &= ~(1<<np);
	if( next_state == state ) ++same;
	else if( equals(dp[next_state],DINF) ) { fail = true; break; }
	else ex += dp[next_state]/3.0;
      }
      if( !fail ) mini = min(mini,((1.0+ex)*3.0)/(3.0-same));
    }
    dp[state] = mini;
  }
  printf("%.10f\n",dp[bitmask]);
  return 0;
}

ここからは2016/6/10に追記:

既に解いていたことをすっかり忘れて再度解いたので解説を追加

ものを倒す順番に意味はないので左から順番にものを倒していくことを考える
f:id:tei3344:20160610013907p:plain
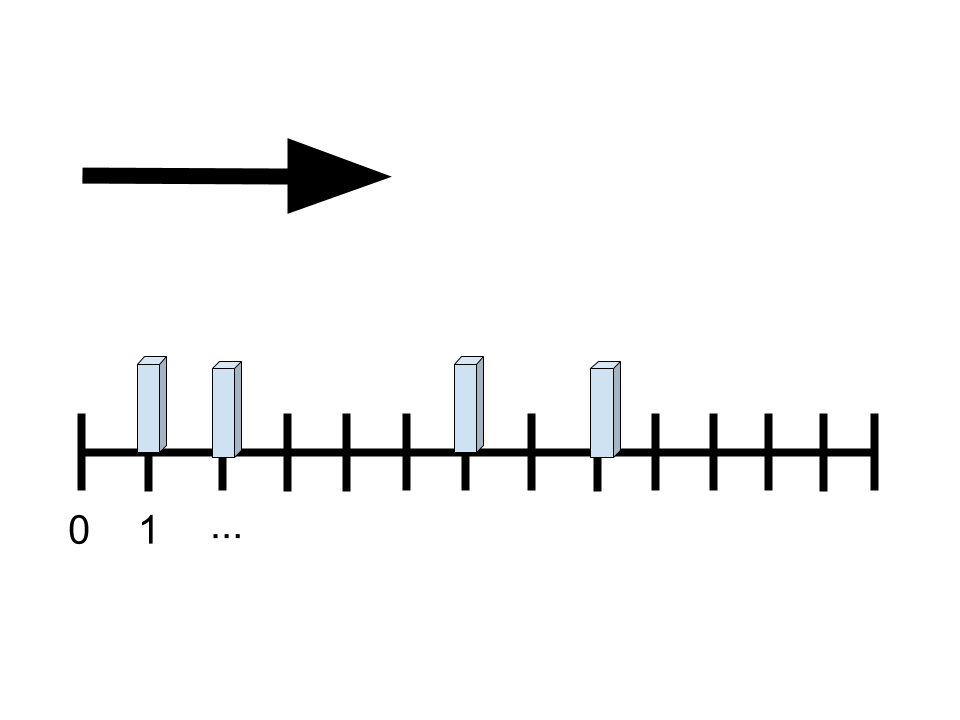
左から順番にものを倒していくので、ボールを投げるべき座標は一意に定まる
その座標は、一番左にあるものの座標をxとしたとき、x+1である
f:id:tei3344:20160610014452p:plain
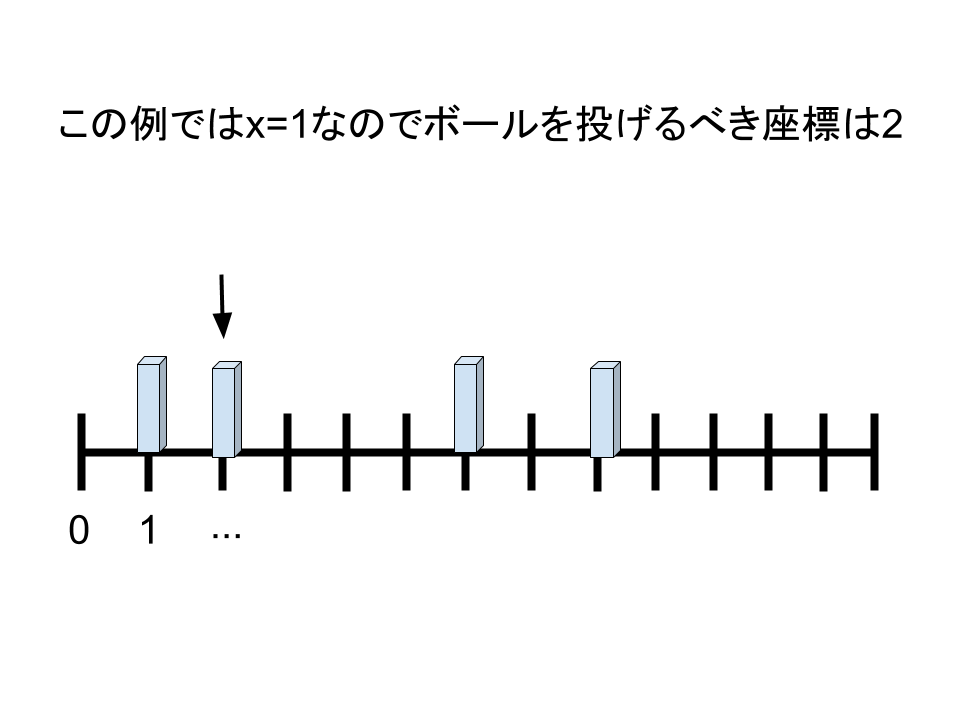
この理由は次の通り
座標xにある物を倒せる座標はx-1,x,x+1のいずれか
しかし、左から順番に倒していくためx-1以下の座標にはものは存在しない
そのためx-1を狙ってボールを投げると、絶対にボールが存在しない座標x-1とx-2にボールが落ちる可能性があり、その分が無駄である
同様の理由から、xを狙ってボールを投げると絶対にボールが存在しない座標x-1にボールが落ちる可能性があり、その分が無駄である
x+1を狙ってボールを投げた場合、ボールが落ちる可能性があるのは座標x,x+1,x+2である
これらの座標にはものが存在する可能性があり、先ほどの２つと比べて無駄がない
そのためx+1を狙ってボールを投げれば良いことが分かる

x+1にボールを投げればよいということが分かった
ここで、x+1にボールを投げた際にボールの落ちる可能性のある場所の状態は次の4通りである
状態1.
f:id:tei3344:20160610015457p:plain
状態2.
f:id:tei3344:20160610015517p:plain
状態3.
f:id:tei3344:20160610015534p:plain
状態4.
f:id:tei3344:20160610015555p:plain

それぞれの状態について考える
状態1.
座標xにあるものを倒すまでに必要な投げる回数の期待値は３である
この期待値は次の様にして求まる
1回目で倒せる確率は1/3
2回目で倒せる確率は2/3 * 1/3
3回目で倒せる確率は2/3 * 2/3 * 1/3
...
n回目で倒せる確率は(2/3)^(n-1) * 1/3
期待値はi回目で倒せる確率*i (1<= i <= ∞)の総和となる
8byteのdouble型で計算することを考えると、(2/3)^500はもう0といっていいくらい小さいことが分かる
なので、先ほどの計算を1から500くらいまで愚直にやってみると良い
すると期待値が3に収束していることを確認できる
手でやるなら式をたてて極限でやれば良い


状態2.
座標x,x+1にあるものを倒すまでに必要な投げる回数の期待値は4.5である
この期待値はサンプル１にある通り（xからx+2までの範囲にたっているものの数が同じであれば状態が異なっても期待値は同じ)
x,x+1,x+2にものが１つしか立っていない状態からそれを倒すまでに必要な投げる回数の期待値は３であることから、
x,x+1,x+2にものが２つ立っている状態からものが１つ立っている状態にするために必要な投げる回数の期待値は1.5であることが分かる ( 4.5 - 3.0 = 1.5 )
この結果を用いて次の様に期待値を求めることができる

座標x+1にボールを投げたとき、
xにあるものを倒せたなら、状態１か状態５に遷移する
x+1にあるものを倒せたなら、状態１に遷移する
これらが確率1/2で起こるので、この時の期待値は
(たっているものの数を2個から1個するための期待値=1.5) +
(xにあるものを倒した後、残り全てを倒すまでに必要な期待値) / 2 +
(x+1にあるものを倒した後、残り全てを倒すまでに必要な期待値) / 2

状態3.
状態2とほとんど同じ
x+1がx+2になるだけ

状態4.
座標x,x+1,x+2にあるものを倒すまでに必要な投げる回数の期待値は5.5
なぜなら、３個立っている状態から１個倒すまでに必要な投げる回数の期待値は１（どこに落ちても必ず１本は倒せるから）
2個立っている状態から1個倒すまでに必要な投げる回数の期待値は1.5なので
3個立っている状態から2個倒すまでに必要な投げる回数の期待値は2.5
1個立っている状態から全て倒すまでに必要な投げる回数の期待値は3なので
3個立っている状態から全て倒すまでに必要な投げる回数の期待値は 2.5 + 3 = 5.5

ものが2個立っている状態から全て倒すまでに必要な投げる回数の期待値が4.5なので、
ものが3個たっている状態からものが2個たっている状態にするまでに必要な投げる回数の期待値は1 ( 5.5 - 4.5 = 1 )
また、座標x+1にものを投げると座標x,x+1,x+2のどれか１個が倒れるので、このときの期待値は
(たっているものの数を3個から1個にするまでに必要な投げる回数の期待値=1) +
(xにあるものを倒した後、残り全てを倒すまでに必要な期待値) / 3 +
(x+1にあるものを倒した後、残り全てを倒すまでに必要な期待値) / 3
(x+2にあるものを倒した後、残り全てを倒すまでに必要な期待値) / 3

これらを再帰的に計算すると良い

コード:

#include<bits/stdc++.h>

#define REP(i,s,n) for(int i=s;i<n;++i)
#define rep(i,n) REP(i,0,n)

using namespace std;

/*
  1->0 : 3
  2->1 : 1.5 2->0 4.5
  3->2 : 1   3->1 2.5 3->0 5.5
 */

int n,x[16];
double memo[1<<18];

double dfs(int bitmask) {
  if( !( memo[bitmask] < 0.0 ) ) return memo[bitmask];
  if( bitmask == 0 ) return 0.0;

  int use = bitmask & -bitmask;
  int x   = log2(use);
  int state = (bitmask>>x&1) | (((bitmask>>(x+1))&1)<<1) | (((bitmask>>(x+2))&1)<<2);
  if( state == 1 ) {
    memo[bitmask] = 3.0;
    return memo[bitmask] += dfs(bitmask&(~use));
  } else if( state == 3 ) {
    memo[bitmask] = 1.5;
    return memo[bitmask] += ( dfs(bitmask&(~use)) * 0.5 + dfs(bitmask&(~(1<<(x+1)))) * 0.5 );
  } else if( state == 5 ) {
    memo[bitmask] = 1.5;
    return memo[bitmask] += ( dfs(bitmask&(~use)) * 0.5 + dfs(bitmask&(~(1<<(x+2)))) * 0.5 );
  } else if( state == 7 ) {
    memo[bitmask] = 1;
    return memo[bitmask] += ( dfs(bitmask&(~use)) / 3.0 + dfs(bitmask&(~(1<<(x+1)))) / 3.0 +
                             dfs(bitmask&(~(1<<(x+2)))) / 3.0);
  }
  assert(false);
}

void compute() {
  int bitmask = 0;
  rep(i,n) bitmask |= (1<<(x[i]+1));
  rep(i,(1<<18)) memo[i] = -1.0;
  printf("%.10f\n",dfs(bitmask));
}

int main() {
  cin >> n;
  rep(i,n) cin >> x[i];
  compute();
  return 0;
}